A compressed sensing framework for perturbation screens
In conventional Perturb-seq, each cell in a pool receives one or more genetic perturbations. Each cell is then profiled for the identity of the perturbation(s) and the expression levels of m ≈ 20,000 expressed genes. Our goal is to infer the effect sizes of n perturbations on the phenotype, which can be the entire gene expression profile (n × m matrix) or an aggregate multi-gene phenotype2,3,11, such as an expression program or cell state score (length − n vector). In both cases, we need O(n) samples to learn the effects of n perturbations (Fig. 1a) (where sample replicates introduce a constant factor that is subsumed under the big O notation), such that the number of samples scales linearly with the number of perturbations.
a, Schematic for conventional perturbation screen with single-valued phenotype. Each sample (yellow) receives a single perturbation (blue). The required number of samples scales linearly with the number of perturbations, as captured by the O(n) term. b, Schematic for compressed perturbation screen with single-valued phenotype. Each ‘composite’ sample (yellow) represents a random combination of perturbations (blue). The required number of samples scales sub-linearly with the number of perturbations given the following: (1) the effects of the perturbations are sparse (that is, k increases more slowly than n), and (2) sparse inference (typically LASSO) is used to infer the effects from the composite sample phenotypes. c, Schematic for compressed perturbation screen with high-dimensional phenotype, which is the main use case for Perturb-seq. The required number of samples scales sub-linearly with the number of perturbations given the following: (1) the effects of the perturbations are sparse and act on a relatively small number of groups of correlated genes (that is, q and r increase more slowly than n), and (2) sparse inference (namely the ‘factorize-recover’ algorithm23) is used to infer the effects from the composite sample phenotypes. d, Two experimental strategies for generating composite samples for Perturb-seq. Both ‘cell-pooling’ and ‘guide-pooling’ change one step of the conventional Perturb-seq protocol. The result is a sample whose phenotype corresponds to a random linear combination of the phenotypes of samples from the conventional Perturb-seq screen. e, Schematic of computational method used to infer perturbation effects from composite sample phenotypes, based on the ‘factorize-recover’ algorithm23. NGS, next-generation sequencing.
Based on the theory of compressed sensing17, there exist conditions under which far fewer than O(n) samples are sufficient to learn the effects of n perturbations. In general, if the perturbation effects are sparse (that is, relatively few perturbations affect the phenotype) or are sparse in a latent representation (that is, perturbations tend to affect relatively few latent factors that can be combined to ‘explain’ the phenotype), then we can measure a small number of random composite samples (comprising ‘linear combinations’ of individual sample phenotypes) and decompress those measurements to infer the effects of individual perturbations. Composite samples can be generated either by randomly pooling perturbations in individual cells or by randomly pooling cells containing one perturbation each (see below).
The number of required composite samples depends on whether the phenotype is single valued or high dimensional. When the phenotype is single valued (for example, fitness), O(k log n) composite samples suffice to accurately recover the effects of n perturbations18,19, where k is the number of non-zero elements among the n perturbation effects (Fig. 1b). When most perturbations do not affect the phenotype, k grows more slowly than n, and the number of required composite samples scales logarithmically or, at worst, sub-linearly with the number of perturbations. Meanwhile, when the phenotype is an m-dimensional gene expression profile, an efficient approach involves inferring effects on latent expression factors and then reconstructing the effects on individual genes from these factors using the ‘factorize-recover’ algorithm23. This approach requires \(O\left(\left(q+r\right)\log n\right)\) composite samples, where r is the rank of the n × m perturbation effect size matrix (that is, the maximum number of its linearly independent column vectors), and q is the maximum number of non-zero elements in any column of the left matrix of the factorized effect size matrix (Fig. 1c). In our case, r is the number of distinct groups of ‘co-regulated’ genes whose expression changes concordantly in response to any perturbation, and q is the maximum number of ‘co-functional’ perturbations with non-zero effects on any individual module. Due to the modular nature of gene regulation20,24,25, r and q are expected to remain small when n increases. Indeed, we observed a relatively small number of co-functional and co-regulated gene groups (small q and r, respectively, relative to n) in previous Perturb-seq screens in various systems2,13. Thus, the number of required composite samples will scale logarithmically or, at worst, sub-linearly with n, leading to much fewer required samples than the conventional approach with large n. In simulations, this result held across a wide range of plausible values for q and r (Extended Data Fig. 1). We provide rough estimates of q and r from our own screens (see below) in the Supplementary Note, section 1.
Experimentally generating composite samples
We generated composite samples for compressed Perturb-seq either by randomly pooling cells containing one perturbation each in overloaded scRNA-seq droplets15 (‘cell-pooling’) or by randomly pooling guides in individual cells via infection with a high multiplicity of infection (MOI)2,16 (‘guide-pooling’) (Fig. 1d). Under certain assumptions, the resulting expression counts in each droplet from either method represent a random linear combination of log fold change effect sizes of guides. When cell-pooling, the expression counts in a given droplet are proportional to the average expression counts of the cells in the droplet, which can then be modeled in terms of log fold change effect sizes of the guides in each cell (Methods). When guide-pooling, the expression counts in a given droplet can also be modeled as the sum of log fold change effect sizes (Methods), although this requires the non-trivial assumption that the effect sizes of guides tend to combine additively in log expression space when multiple guides are present in the same cell. Although higher-order genetic interaction effects can, in theory, bias lower-order effect size estimates in guide-pooled data, we note that only a large imbalance in the direction and/or magnitude of higher-order interaction effects across many perturbations will lead to such biases, and that, even in this scenario, many of the lower-order effects can still be accurately estimated (Supplementary Note, section 2).
Either of the two methods described above can be used to learn the same underlying perturbation effects, but each has different strengths and limitations (Discussion). Guide-pooling has a key benefit over cell-pooling, in that the generated data can be used to estimate both first-order effects and higher-order genetic interactions (with appropriate sample sizes and explicit interaction terms in the model) (Methods). In later analyses, we illustrate the feasibility of estimating second-order effects from guide-pooled data.
FR-Perturb infers effects from compressed Perturb-seq
To infer perturbation effects from the composite samples, we devised a method called FR-Perturb based on the ‘factorize-recover’ algorithm23 (Methods). FR-Perturb first factorizes the expression count matrix with sparse factorization (that is, sparse principal component analysis (PCA)), followed by sparse recovery (that is, least absolute shrinkage and selection operator (LASSO)) on the resulting left factor matrix comprising perturbation effects on the latent factors. Finally, it computes perturbation effects on individual genes as the product of the left factor matrix from the recovery step with the right factor matrix (comprising gene weights in each latent factor) from the first factorization step (Fig. 1e and Methods). Because FR-Perturb uses penalized regression, it is not guaranteed to be unbiased. We obtained P values and false discovery rates (FDRs) for all effects by permutation testing (Methods). In later analyses, we evaluated FR-Perturb by comparing it to existing inference methods for Perturb-seq, namely elastic net regression2 and negative binomial regression16.
Compressed Perturb-seq screens of the LPS response
We implemented and evaluated compressed Perturb-seq in the response of THP1 cells (a human monocytic leukemia cell line) to stimulation with LPS when either pooling cells or pooling guides (Fig. 2a,b). In each case, we also performed conventional Perturb-seq, targeting the same genes in the same system for comparison. We selected 598 genes to be perturbed from seven mostly non-overlapping immune response studies (Supplementary Table 1), including genes with roles in the canonical LPS response pathway (34 genes); GWAS for inflammatory bowel disease (IBD) (79 genes) and infection (106 genes); Mendelian immune diseases from the Online Mendelian Inheritance in Man (OMIM) database with keywords for ‘bacterial infection’ (85 genes) and ‘NF-κB’ (102 genes); a previous genome-wide screen for effects on tumor necrosis factor (TNF) expression in mouse bone-marrow-derived dendritic cells (BMDCs)26 (93 genes); and genes with large genetic effects in trans on gene expression from an eQTL study in patient-derived macrophages stimulated with LPS27 (79 genes) (Methods and Supplementary Fig. 1). We designed four single guide RNAs (sgRNAs) for each gene and 500 each of non-targeting or safe-targeting control sgRNAs, resulting in a total pool of 3,392 sgRNAs (Methods). We introduced the sgRNAs into THP1 cells via a modified CROP-seq vector4 (Methods). After transduction and selection, we treated cells with PMA for 24 h and grew them for another 48 h as they differentiated into a macrophage-like state28, and then we treated them with LPS for 3 h before harvesting for scRNA-seq (Methods). As a baseline, we also collected scRNA-seq data for genetically perturbed cells before stimulation (that is, no LPS treatment) (see Supplementary Note, section 3, and Extended Data Fig. 2 for analysis). For our cell-pooled screen, we used CRISPR–Cas9 to knock out genes2, whereas, for our guide-pooled screen, we used CRISPR interference (CRISPRi) with dCas9–KRAB to knock down gene expression1 (Fig. 2a) to avoid cellular toxicity due to multiple double-stranded breaks in individual cells29.
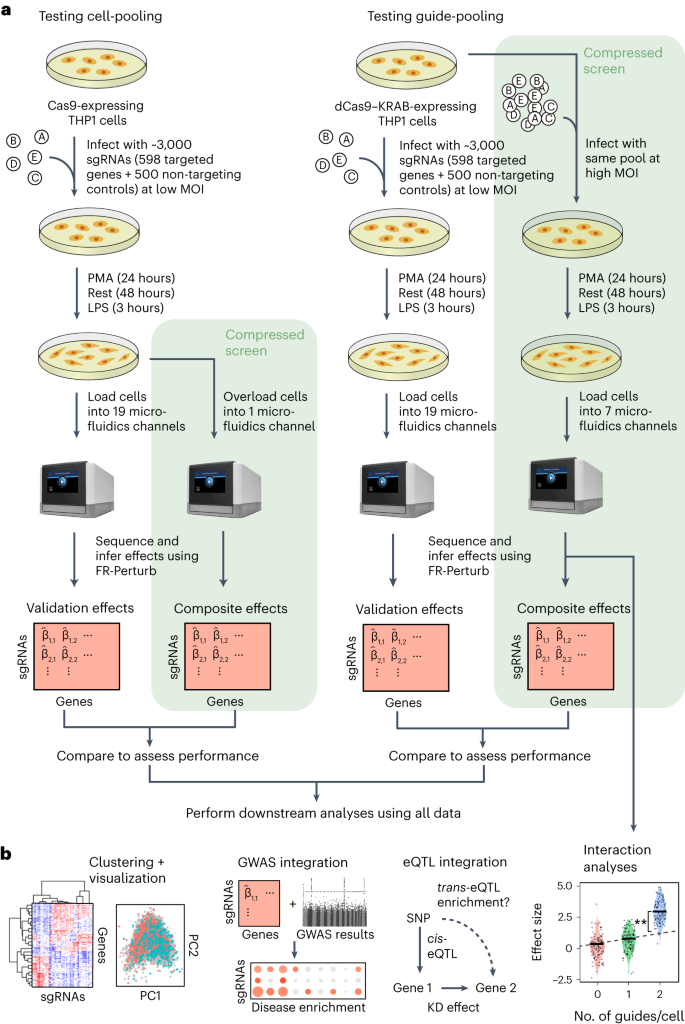
a, Outline of experiments used to test and validate cell-pooling (left) and guide-pooling (right). b, Downstream analyses performed using perturbation effects from all experiments.
By design, the two compressed screens were substantially smaller than their corresponding conventional screens. In the cell-pooled screen, we analyzed a single channel of droplets (10x Genomics; Methods) overloaded with 250,000 cells, whereas, for the corresponding conventional Perturb-seq screen, we analyzed 19 channels at normal loading. We sequenced the library from the overloaded channel to a depth of four-fold more reads than a conventional channel to account for the larger number of non-empty droplets and greater expected RNA content per droplet. After quality control, there were 32,700 droplets containing at least one sgRNA from the overloaded channel (versus 4,576 droplets per channel for a total of 86,954 droplets from the conventional screen) (Fig. 3a), with a mean of 1.86 sgRNAs per non-empty droplet (conventional: 1.11) (Fig. 3b) and a mean of 90 droplets containing a guide for each perturbed gene (conventional: 144) (Fig. 3c). We observed 14,987 total genes with measured expression (conventional: 17,552). Thus, the cell-pooled screen had more than seven times the number of non-empty droplets per channel compared to the conventional screen; considering library preparation and sequencing costs, it was approximately eight times cheaper.
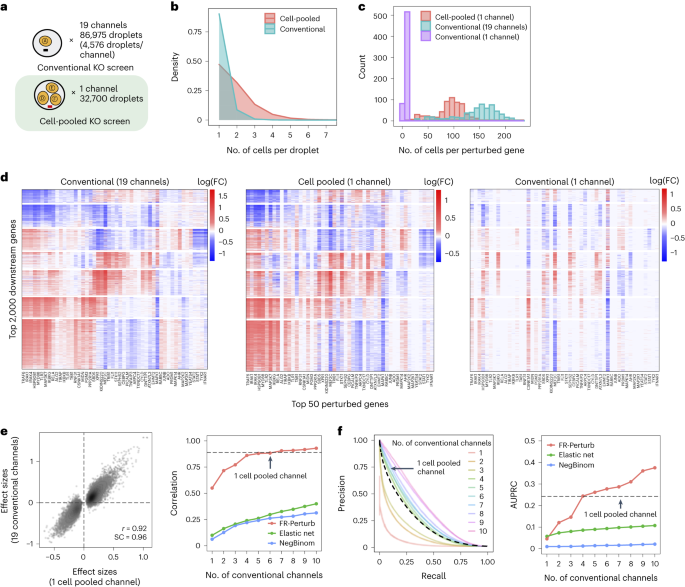
a, Number of channels and droplets from the conventional validation screen (top) and the cell-pooled screen (bottom). b, Distribution of droplets based on the number of cells they contain for the cell-pooled and conventional screens. c, Distribution of the number of cells containing a guide targeting each perturbed gene in the cell-pooled screen and conventional screen (19 channels = full screen, 1 channel = matching number of channels from cell-pooled screen). d, Heat maps of the top effect sizes (inferred with FR-Perturb) from the conventional screen (left), with the same effect sizes shown for the cell-pooled screen (middle) and one equivalent channel of the conventional screen (right). x axis: top 50 perturbed genes, based on their average magnitude of effect on all 17,552 downstream genes. y axis: top 2,000 downstream genes, based on the average magnitude of effects of all 598 perturbed genes acting on them. Rows and columns are clustered based on hierarchical clustering in the leftmost plot. For the left plot, all effects with FDR q > 0.2 are whited out (q value threshold relaxed to 0.5 for the middle and right plots). e, Left, scatter plot of all significant effects (q < 0.05; n = 19,909) from the cell-pooled screen (x axis) versus the same effects in the conventional screen (y axis). Effects represent log fold changes in expression relative to control cells. r, Pearson’s correlation coefficient; SC, sign concordance. Right, held-out validation accuracy of top 19,909 effects (y axis; Pearson’s correlation with validation dataset) from the downsampled conventional screen (x axis) and the cell-pooled screen (dotted line). The same inference method is used to estimate effects in both the downsampled conventional data and validation data. The effects from the cell-pooled screen are estimated using FR-Perturb only (see Extended Data Fig. 3d for results using other methods). f, Left, precision-recall curves computed from downsampled conventional screen and cell-pooled screen (dotted line). True positives = all significant effects (n = 79,100) from the held-out validation dataset. The classification threshold being varied (x axis) is the significance (that is, P value) of the effects. All effects displayed are learned using FR-Perturb. Right, AUPRCs (y axis) computed from the downsampled conventional experiment when varying the number of channels (x axis). FC, fold change.
In the guide-pooled experiment, we infected cells expressing dCas9–KRAB at high MOI (Methods) and profiled a single cell in each droplet across seven channels, whereas, for the corresponding conventional Perturb-seq, we infected cells with the same guide library at low MOI and analyzed 19 channels. From the guide-pooled experiment, we obtained 24,192 cells after filtering (conventional: 66,283), where 35% of the cells (8,448) contained three or more guides (Fig. 4a), with 2.50 guides on average per cell (conventional: 1.13) (Fig. 4b) and 101 cells containing a guide for each perturbed gene on average (conventional: 115) (Fig. 4c). We measured expression for 16,268 total genes (conventional: 18,617). The guide-pooled screen was approximately three times cheaper than the conventional screen.
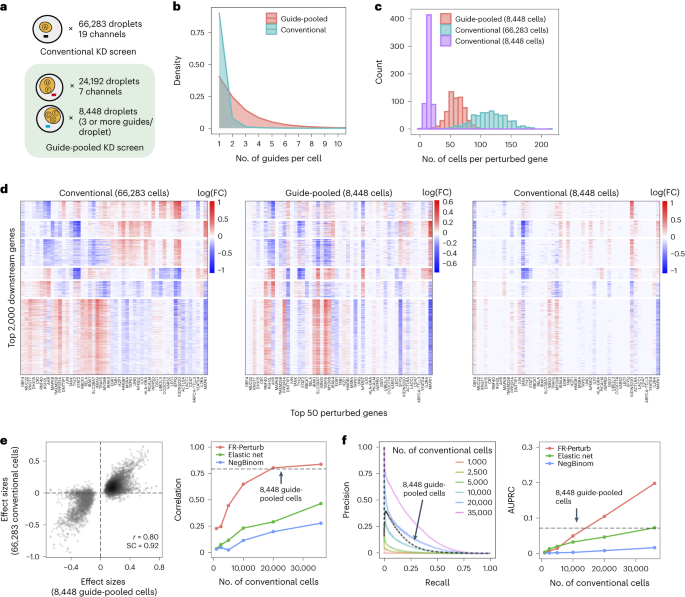
a, Number of channels and droplets from the conventional validation screen (top) and the guide-pooled screen (bottom). We focused our analysis on the subset of 8,448 droplets from the guide-pooled screen with at least three guides per droplet. b, Distribution of cells based on the number of guides that they contain for the full guide-pooled and conventional screens. In practice, we only directly measured the number of guides per droplet rather than guides per cell, but these quantities are equivalent given one cell per droplet. c–f, See captions for Fig. 3c–f. These analyses were conducted in an identical fashion, with the only difference being that the screens are downsampled based on cell count rather than channel count. FC, fold change.
Cell-pooling achieves large efficiency gains
The perturbation effect sizes estimated by Perturb-FR from the cell-pooled Perturb-seq screen (Methods) agreed well with its conventional counterpart. When estimating effects, we included read count, cell cycle and proportion of mitochondrial reads as covariates2, and we combined sgRNAs targeting the same gene while retaining the subset of sgRNAs for a gene with maximal concordance of effects across random subsets of the data (Methods). The significant effects from the compressed experiment (n = 19,909) were strongly correlated with the corresponding effects from the conventional experiment (Pearson’s r = 0.92, sign concordance = 0.96; Fig. 3e). Notably, we observed many more significant effects overall in the conventional screen than the cell-pooled screen (216,220 versus 19,909; FDR q < 0.05), but this is expected given that we intentionally generated a larger and more highly powered conventional screen (144 droplets per perturbation, compared to 90 for the cell-pooled screen) to enable data splitting and cross validation analyses (see below).
The cell-pooled experiment yielded substantially more signal per experimental unit (channel) than the conventional one (Fig. 3d–f). First, the global clustering of effects learned from a single cell-pooled channel was much less noisy than from a single conventional channel (adjusted Rand index of 0.53 versus 0.31 when comparing clusters with those learned from the full conventional screen; Fig. 3d). Moreover, approximately four conventional channels were needed to obtain the same number of significant effects as one cell-pooled channel (Extended Data Fig. 3a). Next, to quantitatively assess the specificity of each approach, we held out half of the conventional data as a validation set, and then we downsampled the remaining half to different numbers of channels and compared the top 19,909 most significant effects learned from the downsampled data (matching the number of significant effects in the cell-pooled screen) to those in the held-out validation set. We found that 5–6 conventional channels were needed to achieve equivalent validation accuracy (correlation) as one cell-pooled channel (Fig. 3e). The relative efficiency gains of the compressed screen were consistent when varying the number of effects being compared (Extended Data Fig. 3c), when comparing effects on modules rather than on individual genes (Extended Data Fig. 4a) or when evaluating performance based on biological informativeness as reflected by the number of effects with significant heritability enrichment for common diseases (Extended Data Fig. 4b,c). We also assessed the sensitivity of each approach by testing whether the significant effects determined from the validation set were recovered by the downsampled conventional or cell-pooled screens. We constructed precision-recall curves, calling ‘true positives’ the 79,100 significant effects from the validation dataset and varying the classification threshold by the significance of the effects in the downsampled conventional or cell-pooled datasets. One cell-pooled channel had similar area under the precision-recall curve (AUPRC) to four conventional channels (Fig. 3f), with consistent efficiency gains when varying the number of true-positive effects (Extended Data Fig. 3c).
Moreover, FR-Perturb substantially outperformed the established inference methods that we tested: elastic net regression2 and negative binomial regression16. Repeating the same analyses as above with each method (Methods), the concordance between the downsampled conventional data and validation data, and between cell-pooled and conventional data, was much higher with FR-Perturb than previous methods (Fig. 3e,f and Extended Data Fig. 3d). FR-Perturb also identified more biologically informative effects than previous methods, based on the heritability enrichment of common diseases (Extended Data Fig. 5). By downsampling the cell-pooled screen, we found that ~1/5 of a cell-pooled channel analyzed with FR-Perturb achieved the same validation accuracy as 10 conventional channels analyzed with existing methods (Extended Data Fig. 3b). We assessed the cost savings of cell pooling over the conventional approach while factoring in sequencing costs in the Supplementary Note, section 5.
Guide-pooling achieves large efficiency gains
Guide-pooled Perturb-seq was also concordant with its conventional counterpart, based on a similar evaluation scheme as above. For the guide-pooled screen, we focused on the 8,448 cells with three or more guides. This number of guides per cell can be achieved with sequential transduction, as done for two of the seven channels (Methods and Supplementary Fig. 2). We learned perturbation effects from both screens using FR-Perturb, with slight modifications to account for differences in the guide-pooled versus cell-pooled screens (Methods). The 5,836 significant effects from the guide-pooled cells were strongly correlated with the same effects from the conventional screen (Pearson’s r = 0.80, sign concordance = 0.92) (Fig. 4e). Thus, even if some nonlinear effects exist between guides, the overall assumption of additivity holds broadly enough to infer many accurate effects. Analysis of the effects that appear to be visual outliers in the guide-pooled screen (Fig. 4e) showed that they arise from correlated noise rather than genetic interaction effects (Supplementary Note, section 4, and Supplementary Fig. 3). As with the cell-pooled screen, the total number of significant effects was much lower in the 8,448 guide-pooled cells versus the full conventional screen (5,836 versus 95,526; q < 0.05), but this is expected because our conventional screen was, by design, larger and more highly powered overall to enable downsampling analyses.
The guide-pooled screen was substantially more efficient than the conventional screen per experimental unit (cell), and FR-Perturb provided more accurate effect sizes than established methods. Around 2.5× more conventionally studied cells were needed to obtain the same number of significant effects as guide-pooled cells (Extended Data Fig. 3e). Globally, the effect size patterns learned from the same number of cells (8,448 cells) were much less noisy in the guide-pooled screen than in the conventional screen (adjusted Rand index of 0.45 versus 0.35 when comparing clusters with those learned from the full conventional screen; Fig. 4d). Approximately twice as many conventional cells were required to learn effect sizes at the same correlation (Fig. 4e) or to attain the same AUPRC (Fig. 4f) as guide-pooled cells when comparing to a held-out validation set. This relative efficiency gain was consistent when varying the number of compared effects (Extended Data Fig. 3g) or when comparing effects on modules rather than on individual genes (Extended Data Fig. 4a). Moreover, the effect sizes inferred by FR-Perturb had substantially better validation accuracy than those from the two established inference methods in both the guide-pooled and conventional data (Fig. 4e,f and Extended Data Fig. 3h). Around 3,200 guide-pooled cells analyzed with FR-Perturb achieved the same validation accuracy as 36,000 conventional cells analyzed with existing approaches (Fig. 2f), leading to an approximately 10-fold cell count and cost reduction over existing experimental and computational approaches (Supplementary Note, section 5).
Guide-pooling is the more impactful compression approach
We conducted a detailed comparison of the strengths and limitations of cell-pooling and guide-pooling relative to each other (Supplementary Note, sections 6 and 7, and Supplementary Fig. 4). Notably, the performance of cell-pooling does not scale with the number of cells per droplet, and the overall efficiency gains of cell-pooling stem from obtaining more non-empty droplets per channel (Extended Data Fig. 6). On the other hand, the performance of guide-pooling does scale with the number of guides per cell, with the best performance attained by cells with four or more guides (Extended Data Fig. 6). This suggests that guide-pooling has the potential to achieve even higher efficiency with a greater degree of overloading than we attained in our experiment.
The effectiveness of compressed Perturb-seq has important implications for existing Perturb-seq screens, each of which already has some overloaded droplets (cell-pooling) and multi-guide-expressing cells (guide-pooling) by chance or by design1,2,13. Although these cells/droplets are often discarded, our results suggest that these cells/droplets can contain even more signal than the single-guide/single-cell-containing ones and, thus, should be retained. To illustrate this, we used FR-Perturb to analyze a Perturb-seq knock-out (KO) screen of 1,130 genes in mouse BMDCs30. In this screen, 519,535 droplets containing a single cell were obtained, of which 33% contained more than one guide by chance. By stratifying cells by the number of guides and comparing the learned effect sizes from FR-Perturb with a held-out validation subset of the data with single guide perturbations, we show that the accuracy of the effect sizes scales with the number of guides per cell and is highest in cells containing three guides (Extended Data Fig. 7a). Thus, by retaining all cells with more than one guide, the sample size of the experiment could effectively be doubled compared to the conventional approach that discards these cells (Extended Data Fig. 7b).
Regulatory circuitry of the LPS response
We next leveraged the overall concordance of all perturbation data (conventional and compressed, KO and knock-down (KD)) to investigate the underlying regulatory circuitry of the LPS response. To maximize power, we merged droplets from the compressed and conventional screens together and then re-estimated all effects. There were 251,792 significant effects in the combined conventional and cell-pooled KO screen (131,161 effects in the combined conventional and guide-pooled KD), an increase of 16% (KD: 37%) over the conventional screen alone. We focused all subsequent analyses on effects from these combined screens.
Overall, the KO and KD screens were concordant, with most of the significant effects (FDR q < 0.05) attributed to relatively few (~5%) of the perturbations, each with widespread effects on many genes (Fig. 5a). As expected, there were substantially more significant effects in the KO screen compared to the KD screen (251,792 versus 131,161 effects), consistent with larger effects of KO on the target gene’s activity31. Effects significant in both screens (n = 26,362) were highly correlated between the screens (r = 0.92, sign consistency = 0.99; Supplementary Fig. 5a–d). The perturbations did not lead to new global cell states, such that profiles from perturbed (one or more targeting guides) and unperturbed (control guide) cells spanned the same low-dimensional space (Fig. 5c). Thus, although many perturbations had significant and widespread effects, they did not yield radically altered phenotypic states, consistent with previous studies of this cellular response2.
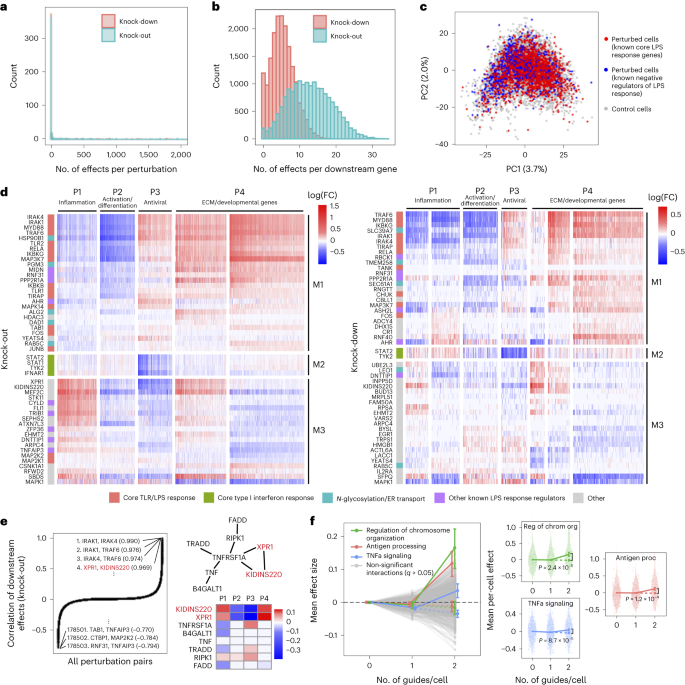
a, Distribution of perturbed genes based on their number of significant effects (q < 0.05) on downstream genes. b, Distribution of downstream genes based on how many perturbed genes significantly affect their expression. c, PCA of perturbed and control cells based on the expression of the top 2,000 most variable genes. Control cells (gray) contain a non-targeting guide only. Perturbed cells (red/blue) contain a guide for one of the following genes. Red: IKBKB, IKBKG, IRAK1, IRAK4, MAP2K1, MAP3K7, MAPK14, MYD88, RELA, TIRAP, TLR1, TLR2 and TRAF6. Blue: CISH, CYLD, STAT3, TNFAIP3, TRIB1 and ZFP36. Numbers in parentheses indicate percent variance explained by PCs. d, Heat maps of perturbation effect sizes (inferred with FR-Perturb) from the KO (left) and KD (right) screens. Rows: top 50 perturbed genes based on the average magnitude of effects on all downstream genes. Columns: top 2,000 downstream genes based on the average magnitude of effects of all perturbed genes acting on them. Rows and columns are clustered using Leiden clustering. Clusters are labeled based on their GO enrichment terms. All effects with q > 0.2 are whited out. e, Left, correlation of KO effect sizes (y axis) between all pairs of perturbed genes (x axis). Top and bottom gene pairs are labeled. Top right, graph of all perturbed genes that physically interact with XPR1 and/or KIDINS220, based on AP-MS data from BioPlex 3.0 (ref. 46). Edges represent physical interaction. Bottom right, mean effects of perturbed genes from top right on P1–P4. f, Analysis of genetic interaction effects. Left, effect sizes relative to control (y axis) of cells containing zero, one or two guides (x axis) within each perturbation module (lines connecting three dots). Modules with significant effects (q < 0.05) are highlighted in color and labeled, with the expected effect of cells containing two guides in the module represented with a dotted line. Error bars represent standard errors obtained from bootstrapping. Right plots, violin plots of the mean effects of individual cells containing zero, one or two guides in the three perturbation modules with significant interaction effects. Dotted line represents the expected effect of cells with two guides. Two-sided P values were computed from permutation testing. FC, fold change.
We organized the perturbations and genes by clustering their effect size profiles (Methods), observing four broad co-regulated programs of downstream genes with correlated responses across the perturbations and three broad co-functional modules of perturbations with correlated effects on downstream genes (Fig. 5d).
The four major co-regulated programs were present in both the KO and KD screens (Fig. 5d), spanning key aspects of the response to LPS: inflammation (P1: cytokine, chemotaxis and LPS response genes; Supplementary Fig. 5e,f); macrophage differentiation (P2: immune cell activation, differentiation and cell adhesion genes); antiviral response (P3: type I interferon response genes); and extracellular matrix (ECM) and developmental genes (P4) (Supplementary Table 2). Inflammation (P1) and the antiviral response (P3) are known to be regulated by LPS signaling through AP1/NF-κB and IRF3, respectively32, and were mostly anti-correlated in their responses to perturbation in our screen, consistent with reports that downregulation of the inflammatory response can lead to upregulation of type I interferon response33,34. Inflammatory signaling is known to lead to macrophage differentiation35, but almost all perturbations with significant effects on inflammation (P1) (in any direction) downregulated macrophage differentiation (P2). This suggests that additional factors beyond inflammatory signaling mediate macrophage differentiation in response to LPS36.
Of the three major co-functional modules, KO/KD of the first module (M1) resulted in strong downregulation of inflammation and macrophage differentiation (P1–P2) and upregulation of the antiviral response and ECM/developmental genes (P3–P4) (Fig. 5d). M1 was mainly composed of core TLR/LPS response genes and genes directly upstream or downstream of the pathway32, including MYD88, IRAK1, IRAK4, RELA, TRAF6, TIRAP, IKBKB, IKBKG, TAB1, TANK, TLR1, TLR2, MAPK14, MAP3K7, FOS, JUNB and CHUK. Given the known function of these genes, we expect that their KO/KD will lead to downregulation of inflammation and macrophage differentiation (P1–P2), as we indeed observed. Other genes in M1 previously shown to downregulate TNF and the inflammatory response when knocked out26 included two LUBAC complex proteins (RBCK1 and RNF31), genes in the OST complex (DAD1 and TMEM258) and ER transport (HSP90B1, SEC61A1 and ALG2) and other genes with diverse functions (MIDN, AHR, PPP2R1A and ASH2L). M1 also included two additional ER transport genes not previously implicated in immune pathways (RAB5C and PGM3), highlighting the important role of N-glycosylation and trafficking in macrophage activation37.
KO/KD of the second co-functional module (M2) primarily resulted in strong downregulation of the antiviral program (P3), with weak/mixed effects on other programs. M2 comprised four genes known to be core components of the type I interferon response38— STAT1, STAT2, TYK2 and IFNAR1—for which downregulation of the antiviral program in response to their perturbation is expected.
KO/KD of the third and final co-functional module (M3) resulted in upregulation of inflammation (P1), downregulation of macrophage differentiation and the antiviral response (P2–P3) and mixed effects on ECM/development (P4). M3 included many genes with known inhibitory effects on inflammation, including ZFP36, an RNA-binding protein that destabilizes TNF mRNA39; enzymes CYLD and TNFAIP3, involved in deubiquitination of NF-κB pathway proteins40,41; pseudokinase TRIB1 and ubiquitin ligase RFWD2, which are involved in degradation of JUN42,43; and RELA-homolog DNTTIP1 (ref. 26). Other genes in M3 included transcription factors (MEF2C, FLI and EGR1), chromatin modifiers (EHMT2 and ATXN7L3) and kinases (CSNK1A1 and STK11).
Interestingly, two of the M3 genes with particularly strong effects on all programs did not have prior immune annotations: XPR1, a retrovirus receptor involved in phosphate export, and KIDINS220, a transmembrane scaffold protein previously reported in neurons44. In the KO screen, this pair of genes had the fourth highest correlation of downstream effects (r = 0.97) among all \(598\choose2\) = 178,503 perturbation pairs (Fig. 5e), following IRAK1/IRAK4, IRAK1/TRAF6 and IRAK4/TRAF6, which are all known to form a physical LPS signaling complex32. XPR1 and KIDINS220 have recently been shown to form a complex that is required for normal regulation phosphate efflux in certain cancer cells45. Furthermore, in affinity purification mass spectrometry (AP-MS) data46, XPR1 and KIDINS220 physically associate with each other and TNF receptor TNFRSF1A. KO of TNFRSF1A in our screen resulted in effects opposite to XPR1/KIDINS220 KO (Fig. 5e), suggesting a possible inhibitory effect of this complex on TNFRSF1A.
We experimentally validated several of the novel results described in this subsection, namely the effects of RAB5C, PGM3, XPR1 and KIDINS220 KO on the inflammatory response in LPS-stimulated THP1 cells, as measured by the secretion of IL6 (Methods). We found that RAB5C and PGM3 KO both led to a modest decrease (~0.85-fold) in IL6 secretion (consistent with our finding that KO of these genes led to downregulation of the P1 program), whereas XPR1 and KIDINS220 KO both led to a substantial increase (~2.6-fold) in IL6 secretion (consistent with our previous finding that KO of these genes led to upregulation of P1; Extended Data Fig. 8).
Guide-pooling reveals second-order genetic interactions
Genetic interactions (non-additive effects) between two or more genes can, in principle, be inferred from cells containing two or more guides, which are generated by chance when transducing cells at low or high MOI (Fig. 4b). Here, guide-pooling can provide increased efficiency compared to the conventional approach, as in the first-order case (Supplementary Note, section 9).
We first attempted to estimate second-order interaction effects and their P values from the guide-pooled screen and corresponding conventional KD screen by adding interaction terms to the perturbation design matrix (Methods). However, although we could generate point estimates of second-order effects2, none of these effects was significant in either screen due to insufficient power (Supplementary Fig. 6a), even with a lax significance threshold (q < 0.5).
To increase power, we aggregated perturbations into modules defined by Gene Ontology (GO) annotations (Supplementary Table 3a) and learned the overall impact of second-order interactions within and between each module on each gene program (Methods). Here, we define an interaction effect as the deviation from the sum of first-order effects for cells that contain any two perturbations from either the same module (intra-module interactions) or two different modules (inter-module interactions) (Methods). To ensure adequately sized groupings, we aggregated perturbations into 490 (possibly overlapping) modules each with at least 20 genes, such that any pair of perturbations in each module was represented in an average of 87 cells in the guide-pooled screen (conventional: 30 cells) (Supplementary Fig. 6b). We also constructed 30 non-overlapping modules by clustering the original 490 modules (Methods), resulting in \(30\choose2\) = 435 module pairs, among which we could compute inter-module interactions. To increase power, we grouped downstream genes by their program (P1–P4) membership (Fig. 5d), computing mean effects on these four programs rather than on individual genes. The results from this analysis represent the extent of intra-module and inter-module interactions on each key program.
We detected three co-functional modules with significant (q < 0.05) intra-module interaction effects on at least one program from the guide-pooled screen (Fig. 5f and Supplementary Table 3b), whereas we detected no significant interactions from the substantially larger conventional screen (even at q < 0.5) (Supplementary Fig. 6c and Supplementary Table 3c). Two of the significant interaction effects—with genes for regulation of chromosome organization (P = 2.4 × 10−5) and antigen processing (P = 1.2 × 10−4)—had insignificant first-order effects on the antiviral program (P3) while having significant positive second-order effects. The third, TNFα signaling, had a significant negative first-order effect on the inflammatory/LPS program (P1) (P = 2.0 × 10−4) and significant positive second-order effect (P = 8.7 × 10−5). This effect is consistent with the reported nonlinear relationship between gene dosage and TNF signaling activity when comparing heterozygous versus homozygous KO mice for either TNF47 or the TNF receptor TNFRSF1A (ref. 48). Interestingly, we did not observe any significant inter-module interactions from either screen (Supplementary Fig. 6d and Supplementary Table 3d,e), which may suggest that perturbations in different modules are less likely to interact with each other49,50.
Integrating Perturb-seq with GWASs
Because dysregulation of innate immune responses plays a key role in many human diseases51, we next asked whether the perturbation effects learned from our in vitro screens can help identify disease-relevant genes and processes. In vitro screens may be especially helpful for this aim given that many of the perturbed genes from our screens are under strong selective constraint in human populations (Supplementary Fig. 7a), making them challenging to directly connect to disease through GWASs52 owing to fewer common variants in or around the gene53,54. To investigate this, we obtained summary statistics from GWAS of 64 distinct human diseases and traits (Supplementary Table 4a), including autoimmune diseases and blood traits as well as non-immune traits/diseases (for example, height, body mass index, schizophrenia and type 2 diabetes). Using sc-linker55, we computed the overall heritability enrichment of these 64 traits/diseases in single-nucleotide polymorphisms (SNPs) in/around genes comprising perturbation modules M1–M3 (Methods). We observed significant heritability enrichment (P < 0.001) for M3 (genes that suppress the LPS response) for two blood traits (lymphocyte and neutrophil percentage), but we did not observe significant enrichment for M1 (positive regulators of the LPS response) or M2 (genes involved in the antiviral response) for any traits (Supplementary Fig. 7b).
Instead, we hypothesized that, if a perturbed gene is important for disease, then disease heritability may be enriched near the downstream genes that it affects12,56. To test this hypothesis, we constructed two ‘perturbation signatures’ for each perturbed gene that include all genes that are significantly upregulated (‘negative’ targets) or downregulated (‘positive’ targets) by its KO/KD. We retained signatures with at least 100 genes, resulting in a total of 1,634 perturbation signatures from both the KO and KD screens. We also constructed signatures corresponding to the gene programs P1–P4 (Fig. 5d). As above, we used sc-linker to test for disease heritability enrichment for each signature/phenotype pair (Methods).
Twenty-three signatures associated with 16 perturbed genes had significant heritability enrichment scores for at least two phenotypes (P < 0.001). In addition, seven phenotypes that reflect immune or blood traits (IBD, eczema, rheumatoid arthritis, asthma, primary biliary cirrhosis and eosinophil percentage) had significant scores for at least two perturbation signatures (Fig. 6a, Supplementary Fig. 7c,d and Supplementary Table 4b,c). As an important negative control, no non-immune/blood traits had any significant enrichment. Most of the significant signatures (15/23) were from the KO screen, suggesting that the expression effects from KO are more suited for this analysis (either because they are more disease relevant or more powered due to capturing more effects). Among the downstream programs P1–P4, we observed significant enrichment from only P2 on three immune traits: IBD, eczema and primary biliary cirrhosis (Supplementary Fig. 7b).
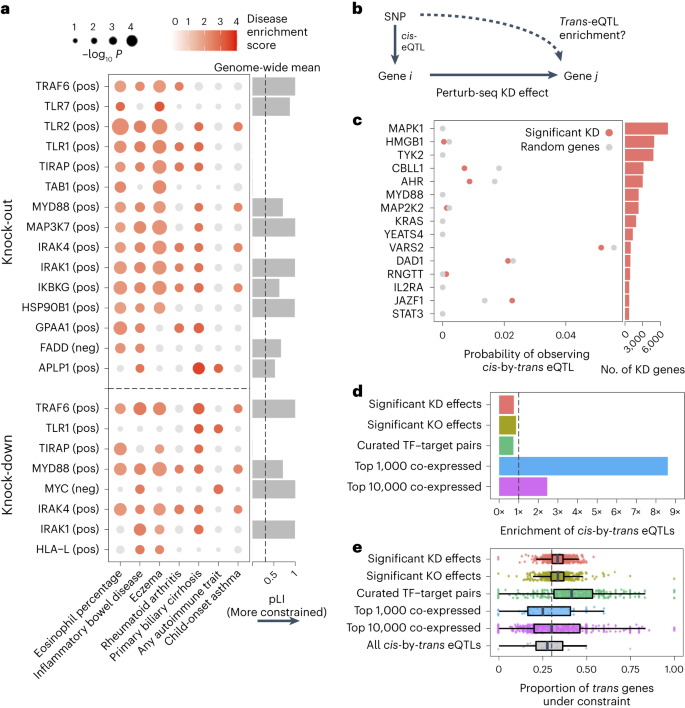
a, Heritability enrichment scores of signatures comprising genes significantly modulated by perturbations (rows) across human traits (columns), computed using sc-linker55. ‘pos’ indicates the set of genes whose expression changes in the same direction as the perturbed gene (that is, downregulated by the perturbation), with the opposite applying to ‘neg’. Displayed are all perturbation signatures and traits with at least two significant (P < 0.001) effects. Non-significant scores are grayed out. Bar plot: probability of loss-of-function intolerance54 (pLI) of the corresponding perturbed gene. b, Schematic of eQTL integration analysis, aiming to test whether trans-regulatory relationships learned from Perturb-seq are also present in eQTL studies. For all gene pairs in which gene i exerts an effect on gene j (that is, has a significant KD effect in our Perturb-seq screen), we would expect that gene i and gene j are enriched for cis-by-trans eQTLs. c, Using data from an eQTL study closely matching our cell type and treatment27, shown is the probability of observing significant cis-by-trans eQTLs among the top 15 perturbed genes from our KD screen and their affected downstream genes (red) compared to random downstream genes (gray). d, Enrichment of significant cis-by-trans eQTLs among various sources of gene–gene pairs: significant KO/KD effects (representing significant gene–gene effects from our KO and KD screens, respectively), curated transcription factor (TF) and target gene pairs65 and the top 1,000/10,000 most co-expressed gene pairs (based on correlation of expression across samples) from the eQTL dataset. Enrichment was computed relative to random trans genes for each cis gene and then averaged over all cis genes. e, Selective constraint on trans genes from d plus all significant cis-by-trans eQTLs from the Fairfax et al.27 dataset. Each point represents a cis gene, whereas the x axis represents the proportion of the trans genes for each cis gene that are under selective constraint (determined as having a pLI >0.5). Box plots represent the median and first/third quartile of points, whereas the bounds of the whiskers represent 1.5× interquartile range.
Most of the significant signatures (17/23) were from genes in core LPS and TLR signaling pathways that fall into perturbation module M1 (even though M1 did not exhibit any direct heritability enrichment itself; Supplementary Fig. 7b): TRAF6 (positive), TLR7 (positive), TLR2 (positive), TLR1 (positive), TIRAP (positive), TAB1 (positive), MYD88 (positive), MAP3K7 (positive), IRAK4 (positive), IRAK1 (positive) and IKBKG (positive). Other significant signatures include HSP90B1 (positive), an ER transport gene important for innate immunity57 that is co-functional with the core LPS genes (Fig. 5d); FADD (negative), a pro-apoptotic gene downstream of LPS signaling that serves for negative feedback32; MYC (negative), an oncogene with known immunosuppressive effects58,59; and poorly characterized pseudogene HLA-L. The two remaining significant signatures are for genes whose functions are not previously associated with the immune system, including APLP1 (an amyloid beta precursor-like gene primarily involved in brain function that, interestingly, contains a missense variant associated with severe influenza60) and GPAA1 (involved in anchoring proteins to the cell membrane). Thus, by leveraging gene–gene links learned from our screens, we were able to identify disease-relevant genes that we were underpowered to detect through direct heritability analyses (Discussion).
To complement our results that focus on common diseases and variants, we also computed the enrichment of Mendelian immune disease genes among the same signatures derived from our screens from above. We found significant enrichment in a similar number of signatures, particularly those with strong effects on the antiviral response (Supplementary Note, section 10, and Supplementary Fig. 8).
Perturbation effects do not concord with trans-eQTLs
Trans-genetic gene regulation (that is, regulation of gene expression distal to the given SNP) has been proposed as a primary mediator of genetic effects on human disease61. Trans-genetic gene regulation can be studied through either population-level genetic data (via eQTL studies62,63) or experimental perturbation of gene expression12, such as the screens conducted in our study. Although both types of data can, in principle, be used to learn the same trans effects, their consistency with each other has not been empirically evaluated.
We, therefore, compared gene–gene regulatory links between our Perturb-seq screen and a trans-eQTL analysis in primary patient-derived monocytes treated with LPS27 (n = 432), closely matching our cell line. For validation, we repeated this analysis using a much larger trans-eQTL dataset (eQTLGen; n = 31,684) although in a model system less similar to ours (whole blood samples). We define a gene–gene regulatory link in eQTL studies based on cis-by-trans co-localization, where a cis-eQTL for gene i is also a trans-eQTL for gene j via a (presumed) trans-regulatory effect of gene i on gene j (Fig. 6b). Here, we assume that a perturbation of a cis-eQTL on the expression of gene i is analogous to the experimental KD in our system. We used coloc64 to compute the posterior probability of cis-by-trans co-localization while accounting for linkage disequilibrium (LD) between SNPs (Methods). To determine whether the regulatory links learned for a given perturbed gene i from Perturb-seq are reflected in the eQTL analysis, we compared the proportion of downstream genes j of gene i in Perturb-seq that co-localize with gene i in the eQTL study, \(P\left(coloc_gene\; i\to gene\; j\right)\), with the proportion of random expressed genes that co-localize with i, \(P\left(coloc_gene\; i\to random\; gene\right)\) (Methods).
Surprisingly, \(P\left(coloc_gene\; i\to gene\; j\right)\) was slightly lower than \(P\left(coloc_gene\; i\to random\; gene\right)\) for individual perturbed genes i (Fig. 6c and Supplementary Table 5) as well as when aggregating across all perturbed genes (Fig. 6d). Moreover, we observed no relationship between either the significance or magnitude of the effect of gene i on gene j and \(P\left(coloc_gene\; i\to gene\; j\right)\) (Supplementary Fig. 9a). We observed similar negative results when obtaining gene–gene links from our KO data or from a curated list of transcription factor–target gene pairs65 (Fig. 6d). Using an alternative way of quantifying gene–gene links in eQTL studies that does not make assumptions about the number of causal variants (that is, bivariate Haseman–Elston regression to estimate genetic correlation of expression66; Methods) yielded similar results (Supplementary Fig. 9b,c). We observed similar negative results when taking cis-by-trans eQTLs from eQTLGen (Supplementary Fig. 10).
Conversely, we did observe significant enrichment of cis-by-trans eQTLs in gene pairs co-expressed in the same eQTL study (Fig. 6d), as has been observed in other trans-eQTL studies62. Notably, co-expression in eQTL datasets is dominated by environmental effects rather than genetic effects67. Thus, given that the two effects are independent across samples, we would not ordinarily expect the most strongly co-expressed genes to be enriched for cis-by-trans eQTLs, suggesting that they may be confounded, in part, by unmodeled technical artifacts or inter-cellular heterogeneity (Supplementary Note, section 11). We also observed that the level of negative selection on the trans gene mirrored the patterns of cis-by-trans eQTL enrichment (or lack thereof) that we observed in the previous analyses (Fig. 6e), suggesting that our power to detect cis-by-trans eQTLs was affected by selection-induced depletion of SNPs affecting the trans genes54,68 (Supplementary Note, section 12).